Zabbix en: un ensayo sobre análisis exploratorio de datos – Parte 2

Introducción

En el artículo anterior, exploramos un poco los conceptos utilizados en estadística básica para estimar los tiempos de respuestas de una aplicación web. En aquel momento, trabajamos media, mediana y 50º percentil, creando el contexto para mejorar el template nativo de monitoreo del nginx y también mostramos los resultados estimulantes de algunos dashboards. Continuaremos nuestro trabajo, pero esta vez analizando la variabilidad de los valores obtenidos durante el monitoreo.

Como este artículo es una continuación de otro, recomendamos la lectura del anterior primero. Sigamos adelante. Te deseo una excelente lectura.

Un poco de estadística básica

En estadística, una distribución de datos tiene al menos 4 momentos:

• Estimaciones de localización
• Variabilidad
• Asimetría
• Curtosis

En el artículo anterior, introducimos el 1º momento, conociendo un poco sobre las Estimaciones de Localización de nuestra distribución de datos; o sea, analizamos algunos valores de los tiempos de respuesta de la nuestra aplicación web. Entendimos, entonces, que los tiempos de respuesta tienen valores mínimos, máximos, medios, y que pueden, o no, ser influenciados por los outliers; o sea, por los picos de un tiempo de respuesta muy bueno o muy malo. Concluimos temporalmente que los tiempos de respuesta varían, pero que podemos conocer un poco más sobre esas variaciones. Vamos, entonces, a entrar en el 2º momento de una distribución de datos: la variabilidad.

Variabilidad

Con la certeza de que nuestros tiempos de respuesta son variables en la mayoría de las veces (o sea, asimétricos), ¿cuáles indicadores de esa variabilidad podemos conocer o trabajar? ¿Cuáles son realmente importantes para nosotros? Y ¿qué pueden decirnos?

En un análisis exploratorio de datos, pasamos a conocer esos indicadores (entre otros), incluso aunque algunos no tengan sentido al final (dependiendo de su aplicación). ¡Sí! Existen casos donde los indicadores pueden no tener sentido para nuestro análisis cuando tenemos otros puntos por considerar o un contexto (o la falta de uno) para ayudarnos a entender mejor sus resultados.

Vamos a trabajar algunos:

• Varianza
• Desviación estándar
• Desviación Media Absoluta (MAD)
• Amplitud
• Rango Intercuartílico – IQR

Amplitud

El concepto de rango es simple y su fórmula también: es la diferencia entre el mayor y el menor valor. En este caso, estamos hablando de una distribución de datos que refleja el período de la hora anterior. Por ejemplo (,1h:now/h), y nos interesa saber el rango de la variación de los tiempos de respuesta de la aplicación web.

Para representar el cálculo del rango en el template “Nginx by HTTP modified”, es necesario crear el siguiente Calculated item:

• trendmax(//net.tcp.service.perf[http,»{HOST.CONN}»,»{$NGINX.STUB_STATUS.PORT}»],1h:now/h)
• trendmin(//net.tcp.service.perf[http,»{HOST.CONN}»,»{$NGINX.STUB_STATUS.PORT}»],1h:now/h)

Dejando de lado el template y la aplicación web, el rango puede ser representado por la siguiente fórmula:

• max(/host/key)-min(/host/key)

Sin embargo, estamos analizando una distribución de datos considerando solamente la hora anterior, por lo tanto:

• trendmax(/host/key,1h:now/h)-trendmin(/host/key,1h:now/h)

El resto de las alteraciones está considerando el uso del template “Nginx by HTTP modified”.

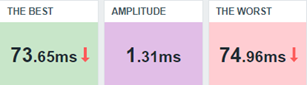
Alterando nuestro dashboard, tendremos la siguiente visión:

La interpretación de este resultado puede ser la siguiente: entre el peor tiempo de respuesta y el mejor, la variación es muy pequeña y nos lleva a entender que durante aquella hora, los tiempos de respuesta se mantuvieron buenos, al principio.

Sin embargo, solo el rango no debe ser suficiente como para diagnosticar la aplicación web en aquel momento. Es necesario combinar ese resultado con otros que veremos a continuación.

Podemos, sí, crear triggers que evalúen ese indicador, como:

• Si en la hora anterior el rango del tiempo de respuesta es mayor que 5 segundos, la aplicación web pudo no haber respondido bien a lo que se le haya exigido.
  • Expression = last(/Nginx by HTTP modified/amplitude.previous.hour)>5
  • Level = Information

• Si el rango es mayor que 5 por 3 veces consecutivas, esto puede significar que constantemente la aplicación web ha sufrido con el desempeño y algo necesita ser investigado, puesto que no es normal que ese tipo de variación se produzca tantas veces, hora tras hora.
  • Expression = min(/Nginx by HTTP modified/amplitude.previous.hour,#3)>5
  • Level = Warning

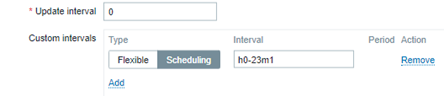
Vale recordar que, si estamos evaluando la hora anterior, no tiene sentido recoger datos cada minuto. Debe utilizase algún tipo de programación para que la métrica sea generada una sola vez, siempre referente a la hora anterior.

De esta forma, las expresiones de las triggers también evaluarán los valores de la forma correcta y evitarán el flapping.

Rango Intercuartílico – IQR

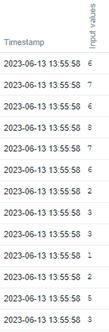
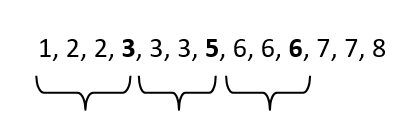
Considera los siguientes valores como ejemplo:

3, 5, 2, 1, 3, 3, 2, 6, 7, 8, 6, 7, 6

Crea el archivo values.txt en tu servidor web y coloca cada uno en una línea. Lee el archivo:

# cat values.txt

3
5
2
1
3
3
2
6
7
8
6
7
6

Ahora, envíalo a Zabbix con Zabbix sender.

# for x in `cat values.txt`; do zabbix_sender -z 127.0.0.1 -s «Web server A» -k input.values -o $x; done

Mira en el frontend de Zabbix el historial de los valores.

Ahora, vamos a crear los Calculated items para 75º percentil y 25º percentil.

• Key: iqr.test.75
  Formula: percentile(//input.values,#13,75)
  Type: Numeric (float)
• Key: iqr.test.25
  Formula: percentile(//input.values,#13,25)
  Type: Numeric (float)

Si aplicáramos en el terminal del Linux el comando “sort values.txt”, la numeración aparecería en orden ascendente. Trabajaremos con este concepto:

# sort values.txt

De izquierda a derecha, avance hasta el 25º percentil. Obtendrás el número 3.

Esta vez, avanza hasta el 50º percentil. Obtendrás el número 5.

Esta vez, avanza hasta el 75º percentil. Obtendrás el número 6.

– El IQR es la diferencia entre el 75º percentil (Q3) y el 25º percentil (Q1). Así excluiremos valores hacia la izquierda (menores) y hacia la derecha (mayores). Esa será la variabilidad entre cuantiles.

Para calcular el IQR en Zabbix, en este caso, haz lo siguiente:

• key: iqr.test
  Formula: last(//iqr.test.75)-last(//iqr.test.25)

Ahora aplicaremos el concepto en el tiempo de respuesta de la aplicación web.

Item calculado para 75º percentil:
key: percentile.75.response.time.previous.hour
Formula: percentile(//net.tcp.service.perf[http,»{HOST.CONN}»,»{$NGINX.STUB_STATUS.PORT}»],1h:now/h,75)

Item calculado para 25º percentil:
key: percentile.25.response.time.previous.hour
Formula: percentile(//net.tcp.service.perf[http,»{HOST.CONN}»,»{$NGINX.STUB_STATUS.PORT}»],1h:now/h,25)

Item calculado para o IQR – Amplitude Interquartil
key: iqr.response.time.previous.hour
Formula: last(//percentile.75.response.time.previous.hour)-last(//percentile.25.response.time.previous.hour)

Mantén la programación para el minuto 1 de cada hora, para evitar que el mismo valor sea generado más de una vez sin necesidad y ajusta el dashboard.

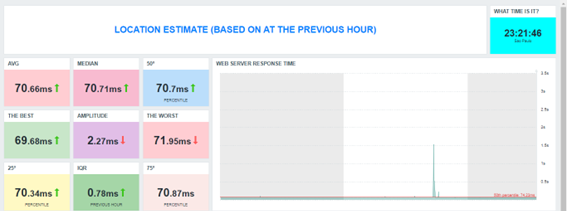
Nota que el RANGO, considerando el peor y el mejor tiempo de respuesta de la hora anterior, trae un valor significativamente “mayor”, en comparación con el IQR. Esto sucede porque en este último (IQR), descartamos los valores demasiado pequeños y los demasiado grandes (outliers) e hicimos nuevamente el cálculo. Entonces, así como existe la media que es influenciada por los valores muy mayores o muy menores, existe la mediana, que representa un valor central y no es sensible a los extremos. También podemos afirmar que el rango es sensible a los extremos, pero el IQR es un indicador robusto que no sufre influencia de los outliers.

Observación: estamos considerando tan solo la hora anterior, pero, intenta imaginar si hiciéramos los cálculos de IQR para todo un día. Intenta aplicar lo que vimos, pero con el time shift 1d:now/d y mira los indicadores del día anterior.

Varianza

La varianza es una forma de calcular la dispersión de datos, considerando su media. En Zabbix, calcular la varianza es sencillo, ya que existe una fórmula específica para hacelo, a través de un Calculated item.

La fórmula es la siguiente:

• Key: varpop.response.time.previous.hour
  Formula: varpop(//net.tcp.service.perf[http,»{HOST.CONN}»,»{$NGINX.STUB_STATUS.PORT}»],1h:now/h)

En este caso, el valor obtenido por la fórmula indica la dispersión de los datos, pero existe una característica en la varianza: en algún momento, se elevan al cuadrado los valores para alcanzar el resultado, y esto altera la escala de los valores que estamos observando en la distribución.

Lo que la fórmula anterior hace puede resumirse en los siguientes pasos:

1º paso) Calcular la media de los datos;
2º paso) Sustraer la media de cada observación;
3º paso) Elevar al cuadrado cada uno de los resultados de las sustracciones;
4º paso) Sumar todos los cuadrados calculados en el paso 3;
5º paso) Dividir el resultado de la suma por el total de observaciones.

En el paso 3, tenemos la alteración de la escala. No obstante, la medida de dispersión todavía se utiliza mucho y puede ser útil para otros tipos de cálculos en el futuro.

Desviación estándar

Es la raíz cuadrada de la varianza.

Note que, si en algún momento la varianza se obtuvo con la elevación de valores al cuadrado, ahora, podemos volver a la escala original de los datos observados.

Existen al menos 2 formas de hacerlo:

1. Utilizar la fórmula para extraer la raíz cuadrada de la varianza:
   1. Key: varpop.previous.hour
   2. Fórmula: sqrt(last(//varpop.response.time.previous.hour))
2. La otra, es usar claves específicas de la versión 6.0 para este tipo de cálculo, con base en la población total de los datos, o tan solo en una muestra:
   1. tddevpop
   2. stddevsamp

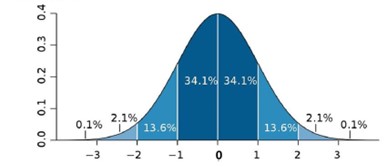
Una forma sencilla de entender el concepto de desviación estándar es: considerando los valores de una distribución ¿cuán lejos de la media se encuentran? Entonces, al aplicar una fórmula específica, llegaremos a este indicador.

Vea:

Esta es una imagen común encontrada en Internet y nos ayuda a interpretar algunos resultados, de los cuales el más básico es el siguiente: Cuanto más lejos de cero esté la desviación, más lejos de la media estarán nuestros valores. Cuanto más cerca de cero, más cerca estarán los valores de la media, por lo que no habrá una gran desviación.

Considera el siguiente Calculated item:

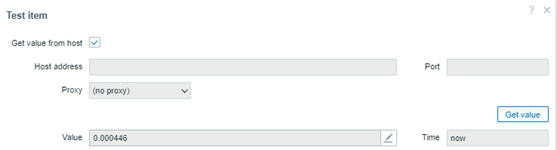
• stddevpop(//net.tcp.service.perf[http,»{HOST.CONN}»,»{$NGINX.STUB_STATUS.PORT}»],1h:now/h)

Estamos calculando la desviación estándar de todos los valores recogidos en la hora anterior, para evaluar si los valores están muy lejos de su media, o cercanos a ella. El resultado:

Considere que el valor no llega a retornar a 1. Se mantiene en 0.000446. Si no llega a tener una desviación, significa que la variabilidad de los tiempos de respuesta de la hora anterior en nuestra aplicación web puede estar con una asimetría baja o moderada, que no hay tantos picos (outliers) y que todo puede estar saliendo como se espera. No obstante, todavía es necesario evaluar otras métricas antes de dar un diagnóstico.

Observaciones importantes sobre la desviación estándar:

• Es sensible a los outliers
• Se lo puede calcular con base en todos los valores de una distribución (población) o incluso, con base en un muestreo
  • Se utiliza la fórmula: stddevsamp. En este caso, podemos obtener un valor diferente de la otra fórmula.

Desviación Media Absoluta (MAD)

Al igual que la desviación estándar, el MAD nos ayuda a entender si los valores de una distribución están alejados de su mediana. La buena noticia es que este indicador de desviación no considera los outliers, por lo que es una estimación robusta.

Atención: si uno de sus objetivos es identificar outliers o considerarlos durante el análisis, la función MAD no es recomendada, justamente porque los ignora.

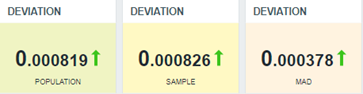
Veamos cómo quedaría nuestro dashboard con algunas de las funciones de variabilidad que estamos estudiando:

Nota que la última está basada en MAD y por esto tiende a tener un valor de desviación menor que las dos primeras, ya que no está considerando los valores de las extremidades (mayores y menores). En este caso, aun así, no tenemos una desviación. Al principio, nuestra aplicación web está manteniendo los tiempos de respuesta dentro de la media.

Dashboard Exploratorio

Conclusión (parcial)

En este artículo, seguimos estudiando sobre los momentos de una distribución de datos, introduciendo el concepto de variabilidad y algunas de las técnicas utilizadas para encontrar indicadores.

Sabemos que los tiempos de repuesta de una aplicación web pueden variar (y sin duda serán bien diferentes entre sí a lo largo de un período) y el estudio de esta variabilidad puede ayudarnos a entender si esta aplicación, específicamente, está teniendo, o no, un buen desempeño.

Claro, este es un ejemplo puramente didáctico y el concepto de distribución de datos, estimaciones de localización y variabilidad pueden ser empleados para el análisis exploratorio de datos considerando un período más extenso, como días, semanas, meses y años. En este caso, es imprescindible utilizar trends en lugar de history.

El objetivo es lanzar luz sobre algunos datos no tan obvios a fin de conocer mejor nuestra aplicación.

En los siguientes artículos, hablaremos de asimetría y curtosis, los 3º y 4º momentos de una distribución, respectivamente.